thermopower in low dimensional systems

Mesoscopic thermoelectric transport near zero transmission energies:

From : Phys. Rev. B 87, 155410 (2013)

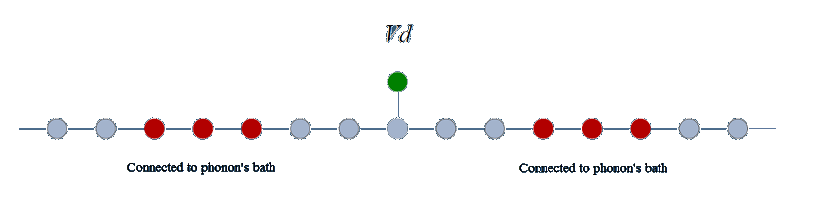
The presence of an off-channel cavity connected to a 1D waveguide leads to the extinction of the transmission at an energy equal to one of the levels of the cavity. Although the energy derivative of the transmission also vanishes at that energy, we can proove by means of L'Hopital theorem  that the Seebeck coefficient does really diverge. This is why we are interested in the investigation of thermopower for this kind of systems. Moreover, in order to have significant figure of merit (ZT), we connect the system to phonon's baths at both sides of the cavity to introduce an asymmetry in the transmission profile. For more details see here.

Scanning gate microscopy of thermopower in quantum point contacts:

Statistics of thermopower in chaotic cavities at the edge of the Hamiltonian spectrum:



We investigate the quantum thermoelectric transport of nanosystems made of two electron reservoirs connected through a low density of states two level chaotic quantum dot , using a statistical approach. Analytical expressions based on an exact treatement of the chaotic behavior in such devices are obtained and analyzed to provide the conditions for optimum performance of the system. We find that the optimum efficiency is obtained for half-transparent dots. This optimum may be enhanced for systems with few conducting modes, for which the exact transport coefficients probability distribution are found to be highly non-Gaussian.

For more details about the power factor statistics, you can check here.

For general techniques about the statistical tools of random matrix theory in thermopower investigation, you can look at  Phys. Rev. B 87, 115147 (2013)