Random matrix theory of quantum transport
|
Do you know,'the devil confided, 'not even the best mathematicians on other planets -all far ahead of yours - have solved it? Why, there's a chap on Saturn -he looks something like a mushroom on stilts - who solves partial differential equations mentally; and even he's given up" .
Arthur Porges -"The devil and Simon Flagg" |
|
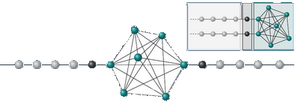
Random matrix theory (RMT) and the quantum electronic transport: The electronic quantum transport through chaotic cavities can be studied analytically and numerically using techniques of Green's functions an scattering matrix approaches. We can investigate the statistics of the quantum coefficients of electronic transport. The RMT provides interesting information on different type of the different physical observables. Among the plenty examples we can provide, we mention:
Some examples could be found in what follows and in some of my articles. |
|
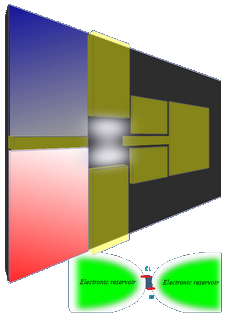
Statistics of the Seebeck coefficient in chaotic cavities at the edge of the Hamiltonian spectrum: By assuming a simple model on a lattice, we investigate the statistics of the Seebeck coefficient at low temperature. A cavity is connected to two semi-infinite 1D leads. We assume that the Scattering matrix of the system is uniformly distributed and taken from the circular orthogonal ensemble. We use the techniques of Greens function to connect the Hamiltonian of the system to the Scattering matrix. We use a trick of decimation method to link the original system two a two level model which seems the right system to describe the physics at the edge of the Hamiltonian spectrum of N level systems. The dependence of the Seebeck probability distribution is obtained analytically and the dependence on the energy is well defined. Other interesting curves of constant behavior are found by taking special rate between the number of levels and the broadening induced by the leads. The mathematical treatment in this work and no approximation (such us the wide band limit) is considered. For more details, you can read Phys. Rev. B 87, 115147 (2013) |
|
Statistics
of the Seebeck coefficient in chaotic cavities at the edge of the Hamiltonian
spectrum:
The aim of this work is to access to the best situation, under some circumstances, for which a system can offer a high figure of merit. We investigate using random matrix theory, the statistics of the power factor at the edge of the Hamiltonian spectrum obtained more easily for tiny systems with small number of levels. We first start by finding the joint probability distribution of the Seebeck coefficient and the transmission and then express the probability of the power factor. We use in this work the concept of minimal chaotic cavities used to investigates the physics of the edge of the spectrum. This allows us to express the desired quantities using only the scattering matrix. The finalresult is interesting since only with the invariance under mathematical transformations, allows one to access to the energy dependence of the probability distribution. All the analytical results are tested numerically and are consistent with the marginal distributions of the Seebeck coefficient or the transmission obtained elsewhere. The result of the article shows that to obtain high power factors, one needs to work at half transparency.The result is easily generalized numerically to higher number of modes in the leads. A Gaussian behavior is detected for very large number of modes which is well tested by numerical fit. More details can be found in statistical analysis of the figure of merit ... |
|
The minimal chaotic
cavity and the edge spectrum statistics:
The concept of the minimal chaotic cavity is very important to investigate the physics of the edge of the Hamiltonian spectrum. The definition is simple: "The minimal chaotic cavity is the system with a number of levels equal to that of the number of the total conducting modes". We state that , at the edge of the spectrum, the statistics of the the physical observable depending on the scattering matrix or/and its energy derivative is the same as in the corresponding minimal chaotic cavity. The proof can be understood by using the concept of decimation procedure in the lattice model of scattering problem. This become obvious for observable depending only on the scattering matrix elements and even in the bulk universality, but works only on the edge spectrum universality for when we investigate expressions containing the scattering matrix energy derivative. We can give as an example the case of the time delays, the Wigner time and the Seebeck coefficient. For more information and details, you can see Eur. Phys. J. B (2013) 86: 117 and Phys. Rev. B 87, 115147 (2013) |